Co-Skewness worth 290bp

This month we look at the impact of different objective functions on the out-of-sample performance of optimised strategy allocations and in particular of the important contribution of co-skewness to the overall skewness of the portfolio for those who care about higher moments.

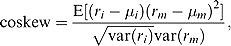
We show that the inclusion of higher moments to your portfolio construction process is worth +290 bp per annum over and above the performance of a broad Hedge Fund Index (Dow Jones Blue Chip Index ). We also show that optimal weights for those who prefer higher odd moments ( Mean, Skew etc ) are generally higher in the direction of those assets exhibiting positive relative skewness of co-skewness with either a benchmark or the portfolio itself.

To illustrate we conduct out-of-sample back testing on the 10 Main Dow Jones CSFB Blue Chip Hedge Fund Strategy Indices from Jan 2006 to Dec 2012. The initial look back period is 24 months and rebalancing takes place bi-annually.

Objective functions used include; maximising the Sharpe ratio, which is equivalent to the classical minimum variance portfolio of Markowitz’s MPT, Maximising the ratio of the CAGR to both the normal, best fit and modified conditional value at risk (CVaR) or Expected Shortfall. This is sometimes called the STAR Ratio. As a control we compare the results to the benchmark index, and both a buy and hold and rebalanced equally weighted index.

The results show that the Modified and Best Fit methods outperform the Minimum Variance / Maximum Sharpe ratio method, the Benchmark Index and both of the equally weighted methods by some margin.

Over the 7 year period the Modified objective function generates an out-of-sample CAGR of +5.7% and the Best Fit +4.84% versus the +1.3%, +2.2%-2.4% and +2.78% of the Minimum Variance, Equally weighted and Benchmark indices respectively.

Of the two methods, we slightly prefer the Best Fit methodology to the Modified method because it produces more diversified portfolios and more conservative Value at Risk numbers.

In the table to the right you can see that both the Best Fit and Modified methods produce less negatively skewed outcomes because they both actively seek to address the asymmetry which the mean variance approach ignores. Indeed it is the very volatility averse nature of the Minimum Variance approach that causes it miss out on the upside volatility in some strategies and during some periods such as the market recovery post 2008.

This is reflected in the %Pos and % Neg numbers where the two better methods have between 5 – 10% more positive returns than the minimum variance ( Max Sharpe ) method and the index itself.

If one looks at the current effective weights ( Jan 2013 weights ) of the different methods you can gain some insight into the strengths and weaknesses of the different methods and of the index itself.

The very volatility averse nature of the Minimum Variance method pushes up its allocations to the lowest volatility strategies such as Multi-Strategy and Fixed Income Arb.

Similarly if you look at the benchmark index weights themselves you can see the lagged effect of legacy allocations to yesterday’s winners such as Event Driven and Managed Futures.

By contrast both the Best Fit and Modified method seek to up weight those strategies that have been showing the most positive co-skewness relative to the index or portfolio. Whether this represents only momentum capture or some evidence of skill is not known but given the relatively low turnovers and high levels of autocorrelation in hedge fund strategies these effects do seem to persist for long enough for some value to be extracted.

As an interesting aside the Effective Weight table on the previous page also shows the Opalesque Emanagers Index has positive co-skewness relative to the Dow Jones CSFB Blue Chip Hedge Fund Index suggesting it would be a complimentary asset to hold in a portfolio.

You can purchase the corresponding spreadsheet here:

Co Skewness and Co Kurtosis Matrices

Buy Now